ローレンツ収縮は相対論において著名な特徴の一つです。しかしものが縮むということの意味は何なのでしょう。わかり切っていると思われるかもしれませんが、案外そうでもないのです。
　少し極端な例を出します。10光年先の星を目指す宇宙船があるとしましょう。かなり光速度に近い速度で飛行しているので、目的地に着くまでに10年とちょっとかかることになります。そして極度に縮んだ状態にあります。
　すぐには到着しない距離の天体を目指すとき、よほど時間が必要なら巨大な船で普通に生活してもらい、世代をつないでいくという方法もありますが、十年程度なら大半の時間を冬眠状態で過ごすことになるかと思います。しかし眠ったままというわけにもいかず、多少の作業はこなすでしょう。その場合もちろん内部で明かりをつけることになると思いますが、その光の速度はどういうことになるのでしょうか。もし縮むということが、基準としての物差しから変わるということであるのなら、例えば10センチ程度にまで縮んだその進行方向に沿うように放射された光は、相当に遅くなるはずです。つまり内部の人間にとっての秒速30万キロメートルは、外部の人間にとっての同じ速度よりは遅い。しかし時間の進みが遅いと先回りして決めてあるのだから、これで何となくつじつまは合う気がします。
　ローレンツ変換式から時間の要素のみを抜き出してみると、Δt’＝Δt√(1-v²⁄c² )となり、ここで移動する者の時間Δt´は静止状態の時間Δtにルート以下の式をかけた値になるということを示します。ｃとvが同じ数値ならば、1－1イコール0で、それを時間が全く進まなくなるということと考えれば（それが物理学や数学の上で無意味であるとかいう理屈はあるのかもしれませんが、わかりやすくする手段です）、移動者の速度vがcに近づくほど時間は遅く進むという意味をこれで読み取ることができます。
　同様に移動者の長さL’はL√(1-v²⁄c²)です。一見して同形であり、つじつまが合うのも道理でしょう。内部の光は確かに遅くなるが、その分長い間飛ぶことができるので同じ距離を稼ぐことができる、という意味になります。
　ところでこれは搭乗者の視線で完結した、あくまで船内の光をもとにした話です。すると、最初の直感、外の光より、内部の光は相当遅いという話はどこに消えてしまったのか。この縮んだ宇宙船が10光年先の天体を目指すというとき、距離がべらぼうに遠くなります。内部の光は遅く、それに従って時間の進みも遅い、と聞かされた時、まず考えるのはこの宇宙船はとても10光年向こうを目指しているとは思えないほどのたくらと動いているということではないでしょうか。
　たぶんこれには一つの返し方があって、逆に移動する宇宙船から見た場合外部の観察者が動いていることになるはずだから、目的地自体が近くなるというものです。外部の観察者は宇宙全体を固定した一つの系とみている、という解釈になります。これに、内部の視点と外部の視点を混同させてはならない、という注釈がつきます。外部の視点で、宇宙船自体の進みが遅いと指摘することは無意味であるという主張です。
　これで、進みの遅い光と、それに応じた宇宙船、そして小さな外部世界という完結した世界ができ上がりました。そして一方に我々が通常考えるところの速度を持った光と、それに応じた広い世界が存在します。こちらもそれ自体で閉じた理論空間です。
　なぜ二つの独立した世界があるのか。何だか狐につままれたような、もやもやの残る結論です。もとはと言えば、宇宙船が縮み、そうであるなら内部でともされる明かりから放たれる光はとても進みが遅いはずである、という仮定から始まったことでした。この仮定は相対論の語る事実として間違いのないところでしょう。では確かにそちら側の光は遅いのです。

“それでは全くつながりのない二つの世界が存在することになるではないか。だからこそ光速度不変の原理が存在する。二つの世界は光速度が等しいことによってつながるのであり、そこに変換式が存在する根拠があるのだ”

……一つ理屈を考えるなら、そういうことになるのかもしれません。ほかの形もあり得るのでしょう。もちろんこの時点で、はっきりとその理屈は間違いであり、明白なでたらめであると私は断定しますが、案外そうはとらえない人が多いことも事実です。
　相対論に批判的な人の著書を何冊も読んできて、基準系とそれに対して運動状態にある系とを図示し、座標が違うのだから一つの線で結んではいけないとか、共通の計算式は成り立たないとか、丁寧に説明してあるものをいくつか見ましたが、あまり納得は得られていないようです。
　間違っていると思いつつも、私は相対論支持者の言い分が分からないでもありません。一つの線で結んではいけないといわれても、そもそも一つの線で結ぶという主張なのだし、計算式は成り立たないというが、それをちゃんと提供するのが相対論ではないか、ということです。

　エレベータの例も列車の例も、外と一続きの空間であるからこそ起きる現象でした。そこを閉鎖空間ならではの出来事と誤解し、もっともらしい語りを用意する。わかってしまえば単純極まりない子供だましの理屈にすぎません。ただ、宇宙船の例はもう一段複雑であり、内部が閉鎖空間であることを超えた、奇妙な逆転が生じています。つまり外部の傍観者の方も閉鎖空間に置かれ、二つの世界が並立しています。それぞれが無矛盾であれば、それで納得してしまうことは当然あり得ます。
　エレベータと列車の、二つの思考実験の場合には、内部が独立した空間であることは無意識裡の前提です。したがって内外が連続的であることを示せば、ある程度こちらの言い分に納得してくれる人もいるかもしれません。しかし内部が独立空間であるという積極的な主張をする相手に、「いや内部を独立的に語ることはできない」と言って、それで引き下がる人はまずいないと思われます。列車の思考実験の場合には中央で光が出会うという小細工のおかげで同時性のずれという虚構が示せたわけですが、すでに時間も巻き込んだ形で独立性が主張されているとき、同時性の概念を持ち込んでの説得もあまり効果が見込めません。

　ここで、あっけにとられるような回答をまず示しておきます。宇宙船が縮んだ形になったら、それはまともに飛ぶはずがない、というものです。ぺちゃんこにつぶれた自動車がまともに動くはずはないし、縮んだ列車も走るわけがない。それと同じです。なぜこの当たり前の事実をだれも言わないのでしょうか。
たとえば高速移動中のものは進行方向に縮む。このことは、相対論の帰結としては有名な部類です。では精密で古典的な機械、懐中時計を高速移動させたらどうなるか。まあ、デジタルデバイスでもよいのですが、直感的にわかりやすいもので考えることにします。
　懐中時計を用意し、文字盤を真正面から見据える形にして、左右どちらかの方向に動かすと、これは左右につぶれた、いびつな円形になります。

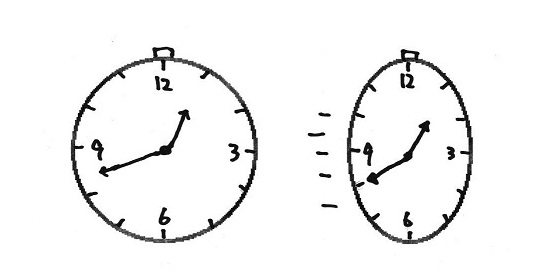
　では、右に示した側は、中の歯車もいびつな円形になるはずです。それでどうして時が刻めるのでしょうか。いびつな円形への変化が真に物理的な効果を伴うものであれば、または物理的な原因によるものならば、いびつな円形の歯車を正確にかみ合わせて、なおかつ縦長の形状を維持したままで回すことなどできません。相対論には少なくとも、そういう奇怪な現象を支持する式は存在しないはずです。ここを間違ってはなりません。あるのは、進行方向に縮むという計算式だけです。　
　この先の弁明は予想できます。一つは、時計全体が歯車と同じ比率で縮むのだから、動きの正常性は保たれる、というもの。それに対しては、いびつな円形の時計にいびつな円形の歯車を仕込んだところで動きはしないと答えます。これはさすがに論外であると言えるでしょう。
　多少厄介なもう一つの方は、ものが縮むとは空間自体の縮みの反映なのだから、時計にとって真円であるものが傍観者の私にとっていびつな円であることと両立するのである、というもの。では、私にとっていびつな円であることを認めてくれるのです。ならば、残念ながら私のいる宇宙ではすべて同じ向きに長軸をそろえたいびつな円形の歯車の組み合わせで時計を作ることはできないし、歯車を回転させてなお縦長のままであることも不可能です、と答えることにしましょう。ただ、抽象的議論の難しいところで、おそらくこの簡単明瞭な説明は多くの人にとって明白すぎるゆえにかえって幼稚であると片付けられてしまうかもしれません。
　この場合の相対論的な見方をもう少し小難しく言い直すなら、私の持つ時計が他人の目から見ていびつであることは、何かの確定的な、できれば力学上の意義を持ち得るということです。

　まず、他人の目で見てのいびつさが私の持つ時計にとって無意味であることは明らかでしょう。それは実は、周りに立っている人たちがこれをいろいろな角度から見て、長方形に見えたり、ラグビーボールのように見えたりすることが、この時計の進み方に変化を与えないことと同じなのですが、この意見は素直に了解しにくいものだと思います。相対論はもう少し深い意図のもとに「いびつに見える」と言っているように感じます。
　実際に、周りの人たちが時計をいろんな形に見るということに、時計自体のさまざまな物理量の変化を伴うということは意図されておりません。相対論は明らかに物理量の変化を要求しています。時間が遅く進むように見える、縮んで見える、という主張は、単純に見るということではなく、明らかに物理的な理論関係に置くということを意味します。だからこそ誰も目撃できないビッグバンは実際に起きたのであり、まだ発見されないブラックホールもブラックホールであるのです。いずれも、理論により導かれた事実です（ここではまだ形而上学としての事実ということを考えず、単純な科学的主張ととらえておきます。つまり人間のように、それをビッグバンと認識する存在が登場するまでは、ビッグバンそのものも起きてはいなかった、とする理論もあり得るのです。冗談みたいな話ですが、こういうところまで検討する必要があるかもしれないと思う程度には、相対論も空想的なのではないでしょうか）。
　同様に、宇宙船が無人探査機であったとしても時間の遅れは生ずるし、移動する無人の列車は縮む、と考えてよいのでしょう。つまり、私以外の視点からこの時計がいびつであることが意義を持つなら、その位置に視点を持つ人が確実にいることとは無関係に、その効果が現れなければならないのです。
　地球を変形した形で見ることが可能な程度には高速である運動体が宇宙の中には多数存在します。そしてこの地球上には多数の機械仕掛けがあるわけですが、しっかりメンテナンスされていればおおむね正常に作動します。例えば私の懐中時計の歯車に、他からの視点でゆがみが生じたから刻みが止まった、などという事例は聞いたこともありません。すなわち、私の持ち物である時計の動きが他の視点からの見え方に依存しないことは事実上無限回数の検証を経ていると言えます。この「見え方」を、ここまでの文脈のように理論的関係とせず、実際に見ることと置き換えても変わりはないと思います。あまり高速で動かすと壊れてしまうので、私が静止状態のまま、超高速で移動するカメラか何かでとらえることを想像していただけばよいでしょう。時計が動くか動かないかは、私が見て真円の歯車を持つかどうかだけで決まるのです。
　逆にある特定の相対速度を持つ視点に対してのみ、真円に見えるように計算されたいびつさを持つ時計を作り、動かないことを承知で動力も仕込んでやったとした場合、ほとんどの人にはガラクタですが、それを真円に見ることができる人のみはこの時計の動いているところを見ることができるのでしょうか？　答えは明らかにノーでしょう。ではその逆の場合の、私がある人の時計を進行方向にいびつにつぶれた形に見ることは、その時計に対して意味があるのでしょうか。もちろん立場が変わるだけなので同様に無意味のはずです。最後に、歯車を真円とみる持ち主には気づけないが、歪みを見る私にはわかる何かがこの上にあるでしょうか。常識的に考えて、私だけに関知され得る物理的な変化は存在しないように思います。私にわかるなら、当事者である持ち主には､別の表現形ではあるかもしれないが、必ず何らかの変化が告知されるのではないでしょうか。例えば地球がいささか扁平であることは、地球外からしか見えませんが、正確な計測や、重力の強さの違いによってそこに住む我々にも理解できるものになります。
　時計についての以上の説明にはもちろん唯一の例外があります。「他人からはいびつに見える」というその一点のみ、視点の変化が有意義となります。しかしそれはたとえば十円硬貨が角度によって楕円に見えたり棒状に見えたりするが、よく確認するならおなじみの円盤形であることがわかるという、日常感覚で対処できるありきたりな意味であり、それを超える深遠な事実など何一つ存在しません。だが相対論はそれがあると言い、信じてしまう人が多数です。なぜそうなってしまうかは改めて考えるべき問題ではあります。ただ、高速移動しながら私の時計をゆがんでいると見る視点がいくつも想定できるとして、それで私の時計が動かなるということが考えられるか、逆に私が相手の時計を見ただけでなぜか停止するということがありうるのか、そういうことをまずは常識的に考え直してみることが必要かと思います。